TR-PAC determination of bond dissociation enthalpies
Even if we are not at all interested in obtaining kinetic data, TR-PAC has advantages in relation to classical PAC. Recall the example of the determination of a R—H BDE in an organic molecule using the di-tert-butyl peroxide strategy:
| t-BuOOBu-t (sln) |
(8) | |
| 2 RH (sln) + 2 t-BuO• (sln) → 2 R• (sln) + 2 t-BuOH (sln) | (9) |
Unlike PAC, TR-PAC allows to discriminate between the two reactions, so we can determine each enthalpy individually [1]. The O—O bond is instantaneously cleaved by the laser pulse, so the first reaction will always correspond to a very fast process. The second reaction, however, is a second order process. Depending on the concentration of the substrate RH, it can either be fast enough to be handled by the classical PAC procedure described in the PAC determination of bond dissociation enthalpies section, or made to fit in the intermediate regime. In this case, the TR-PAC methodology affords the separate magnitudes of each sequential process (Φobs,1 and Φobs,2), from which the corresponding observed enthalpies can be calculated using eq 14. To relate these with the enthalpies of the corresponding reactions, eq 6 is used, yielding [2]:
| (16) | ||
| (17) |
Note that only the first step is light-initiated. Therefore the laser energy Em does not appear in eq 17, which results from the energy balance of the second process. However, the yield of this sequential step is still dependent on the yield of the first, i.e. the quantum yield Φr.
Now, since it is the R—H BDE that we are after, we can dismiss the calculations regarding the first reaction. Indeed, the enthalpy of the second reaction is simply twice (each laser pulse originates two tert-butoxyl radicals, that subsequently attack two RH molecules) the difference between the R—H and t-BuO—H BDEs (see Bond Dissociation Energies chapter). Therefore, if we know the latter, we can obtain the desired BDE from the direct determination by TR-PAC of the enthalpy of the second reaction [2].
| (18) |
This is where the investment made on the more complex mathematical analysis of TR-PAC begins to pay off: the second reaction (9) is much easier to interpret than the overall reaction (10, compare eq 18 with eq 11). However, we do need an accurate value for the BDE of t-BuO—H in the same solvent (recall that PAC and TR-PAC afford BDEs in solution). Several methods are available to obtain that value, but it suffices to say for now (this matter will be expanded below) that such values are available for the most common organic solvents [3].
Another big advantage of TR-PAC is explained through eq 17, where ΔrV2 represents the molar volume difference between products and reagents in reaction 9 alone. Unlike the di-tert-butyl peroxide homolysis (and the overall reaction 10), the number of reactant molecules in reaction 9 equals the number of product molecules, so that its volume change should be rather small [4]. This means that by using TR-PAC we can neglect the volume change correction altogether, by making ΔrV2 = 0 in eq 17 [2].
TR-PAC has yet another important advantage: it widens the scope of photoacoustic calorimetry by allowing to investigate reactions that cannot be studied with classical PAC, simply because they are too slow [5,6].
Even very fast reactions can be advantageously probed with TR-PAC, since it allows to work with more dilute solutions of the substrate RH (recall that the rate of reaction 9, and hence of the overall reaction 10, is proportional to the concentration of RH) [7]. This makes possible to study some substrates which would be either too scarce or too expensive to be used in classical PAC experiments. Moreover, the use of dilute solutions also helps to increase the overall accuracy of PAC determinations, since many equations and assumptions used are strictly valid only for that limiting case.
Before ending this section, lets return to the determination of t-BuO—H BDE in solution. One of the methods available is the study, by classical PAC, of the di-tert-butyl peroxide homolysis itself. The approach involves the determination of the enthalpy of reaction 8 alone, which coincides with the O—O BDE in di-tert-butyl peroxide. Using a thermodynamic cycle, we can relate that O—O BDE to the enthalpy of formation of t-BuO•, and then to the desired t-BuO—H BDE, as indicated in eq 19 [2].
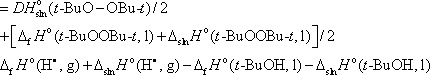 |
(19) |
This exercise is similar to the one presented in the PAC determination of bond dissociation enthalpies section. As an example, we can simplify eq 19 in the same manner as eq 11 for the case of benzene as the solvent, yielding eq 20.
(20) |
Again the solvation enthalpy of the hydrogen atom was left out, so that it cancels when the gas-phase value of the R—H BDE is calculated from the solution-phase BDE of eq 18.
